Интерес к нейронным сетям
— В ряде работ ,, указано, что на сегодняшний день наиболее распространенными моделями прогнозирования являются авторегрессионные модели (ARIMAX), а также нейросетевые модели (ANN). В статье , в частности, утверждается: «Without a doubt ARIMA(X) and GRACH modeling methodologies are the most popular methodologies for forecasting time series. Neural networks are now the biggest challengers to conventional time series forecasting methods».
— Без сомнений модели ARIMA(X) и GARCH являются самыми популярными для прогнозирования временных рядов. В настоящее время главную конкуренцию данным моделям составляют модели на основе ANN.
У нас на сайте пока опубликован только один материал, посвященный нейронным сетям, в котором я давала советы по созданию сети. Интерес со стороны читателей заставляет меня более активно заниматься нейросетевым прогнозированием. Давайте попробуем шаг за шагом проделать работу по созданию, эффективному обучению и адаптации нейронной сети с тем, чтобы разобраться в нюансах нейросетевых моделей прогнозирования.
Результаты
Переделав пример Хайкина под нужны прогнозирования торгового графика (энергопотребления), мы получили новую нейронную сеть, трехслойную, полносвязную. Все параметры сети были из примера по книге Хайкина.
Созданная нейронная сеть обучается очень быстро: от 60 до 120 секунд в зависимости от мощности компьютера.
При тестовом прогнозировании на созданной нейронной сети получается прогноз торгового графика на сутки вперед с ошибкой MAPE ≅ 4%.
Исходный пример из книги Хайкина, а также мой пример нейронной сети для прогнозирования торгового графика европейской территории РФ с исходными данными вы можете скачать по приведенным ссылкам и попробовать решить свою задачу.
Нейронная сеть
1. Познакомьтесь с нейронной сетью.
Что делает нейронная сеть? Его наиболее важная функция — использовать для сквозной классификации. Классификация изображений и жанров текстов заключается в том, чтобы вводить контент, который необходимо классифицировать, в модель в виде числовых векторов, а затем классифицировать их с помощью операции черного ящика, о которой мы упоминали выше. Результат классификации значения или вектора. В качестве простого примера: при распознавании рукописных чисел входным слоем является матрица пикселей изображения 28 × 28, а выходным слоем — Такая однорядная матрица, первый столбец равен 1, что означает, что результат классификации равен 1, а скрытый слой посередине — это наш черный ящик.
2. Модель нейрона.
Самым основным компонентом нейронной сети является нейрон. Наименьшей единицей на уровне активации ввода и вывода является нейрон. На следующем рисунке показан процесс анализа модели нейрона. Нейрон получает m внешних входов. Сигнал (может быть один или несколько, передаваемых другими нейронами), сначала взвесьте все сигналы, а затем оцените, превышает ли он пороговое значение нейрона, если оно больше порогового значения нейрона, отправьте его в функцию активации для вывода, как показано на следующем рисунке. Сетевая структура модели нейрона.
3. Одноуровневая сеть
Правило обучения нейронной сети состоит в том, чтобы соответствовать функции путем настройки весов и пороговых значений. Эта настройка зависит от размера предыдущего значения возбуждения нейрона. Как показано на рисунке, это однослойная нейронная сеть (персептрон). Она регулируется путем настройки трех весов. Вы можете подобрать несколько простых функций линейной классификации.
4. Многослойная сеть
Если перцептрон имеет только один слой, его способность к обучению очень ограничена. При изучении нелинейных задач, поскольку модель не может найти подходящие веса, вес будет колебаться. Если рассматриваются нелинейные задачи, необходимо несколько слоев. Сеть, то есть добавляет несколько скрытых слоев между входным и выходным слоями. Другими словами, многослойная сеть непрерывно увеличивает широту функции аппроксимации с помощью функции активации, и ее, очевидно, легче классифицировать с помощью нелинейной функции, как показано на рисунке. Многослойная сеть с четырьмя скрытыми слоями (см. ) и пример линейно неразделимой задачи.
5. Алгоритм обратного распространения ошибки (BackPropagation)
Способность к обучению многоуровневой сети намного выше, чем у одноуровневой сети, но ее обучение очень проблематично. Обычно используемый метод — это алгоритм обратного распространения ошибки, также называемый алгоритмом обратного распространения. Следующий рисунок в этом разделе содержит скрытый слой Сеть является примером для ознакомления с принципом BP.
5. Возникла проблема
Количество скрытых слоев нейронной сети достаточно, чтобы соответствовать любой сложной функции, но часто происходит переоснащение.Существуют две стратегии для решения таких проблем: одна — установить обучающий набор и проверочный набор, когда ошибка обучающего набора Если она уменьшается, но увеличивается ошибка набора проверки, прекратите обучение; второй тип — регуляризация. Вы можете добавить условия регуляризации L1 или L2 к функции потерь, чтобы описать сложность алгоритма. Подробнее см. «Методы статистического обучения» учителя Ли Хана. ».
Прогнозирование с помощью нейронной сети
Я взяла данный пример реализации нейронной сети, просмотрела внимательно содержание его функций и сделала свою нейронную сеть, которая прогнозирует торговый график по европейской территории РФ (далее ТГ) на 24 значения вперед. В архиве вы можете скачать, как полученный мною пример, так и исходные данные к нему. Основной файл называется Create_ANN_step_1.m
Шаг 1. Инициализация и исходные данные
Исходные данные по торговому графику содержатся в файле VOLUMES_EUR.mat и имеют значения за период с 01.09.2006 до 22.11.2011.
Обучение сети, то есть определение весов и смещений для всех нейронов я выполняю на периоде значений с 01.01.2010 по 31.12.2010.
В качестве тестового я выбрала период с 01.01.2011 по 22.11.2011.
Шаг 2. Предварительная обработка исходных данных
Из теории и из примера Хайкина я понимаю, что нейронная сеть работает со значениями временных рядов от 0 до 1. Исходные значения торгового графика в массиве VOLUMES_EUR, конечно, выходят далеко за этот диапазон. Для использования нейронной сети необходимо предварительно отмасштабировать исходный временной ряд, как показано на рисунках.
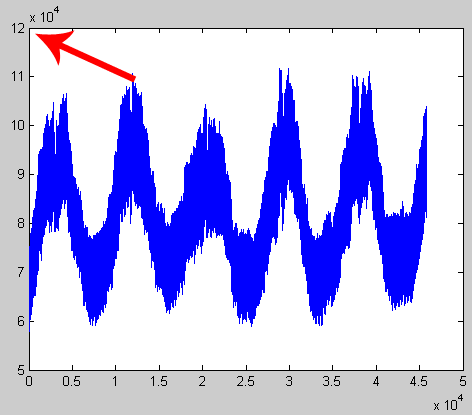
Рис 1. Предварительно мы имели значения от 57 847 до 111 720.
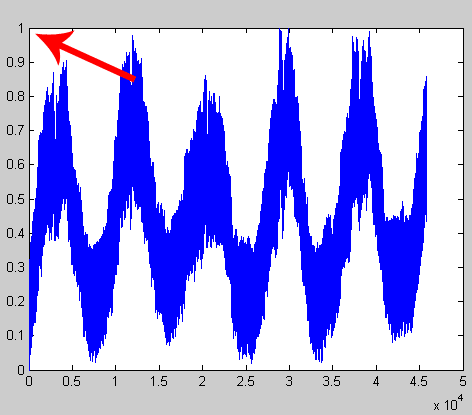
Рис 2. После масштабирования мы стали иметь значения от 0 до 1.
Шаг 3. Настройка нейронной сети
Так как в примере Хайкина содержалась трехслойная полносвязная нейронная сеть, то я на ней остановилась. Кроме того, из статей я знаю, что для прогнозирования энергопотребления чаще других используется именно трехслойная архитектура.
На вход нейронной сети я подаю 48 значений ТГ за двое предыдущих суток, скрытый слой после нескольких попыток стал содержать 72 нейрона, а на выходе мы получаем 24 прогнозных значений торгового графика на будущие сутки. Структура нейронной сети получилась следующая.
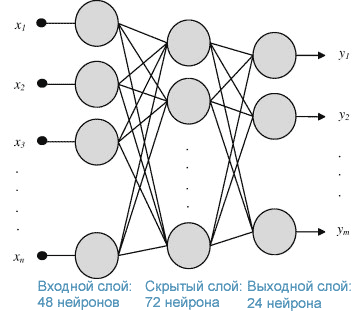
Рис 3. Структура разработанной нейронной сети.
После описания структуры указываются значения нескольких параметров нейронной сети (см файл Create_ANN_step_1.m). Не мудрствуя лукаво, оставила все значения, которые были установлены в примере Хайкина.
Шаг 4. Обучение сети
Двойной цикл по эпохам и внутренней корректировки весов я взяла в чистом виде из примера Хайкина. Такое обучение называется обучением нейронной сети по методу back propagation error (обратное распространение ошибки). Изменения внесены только в части формирования входа и выхода нейронной сети. Общие комментарии по ходу алгоритма приведены в тексте программы.
Шаг 5. Тестовое прогнозирование
На пятом шаге я формирую тестовый массив «T» и прогнозирую на полученной нейронной сети. Все прогнозирование в итоге сходится к нескольким строчкам кода.
% Вход i1 = T((i-1)*24+1:i*24,2); i2 = T((i-1)*24+1:i*24,3); input = i1; i2; % Прогноз outHiddenLayer = bpm_phi(W1 * input + b1); outOutputLayer = bpm_phi(W2 * outHiddenLayer + b2); % Переменная результата Result((i-1)*24+1:i*24,1) = outOutputLayer;
По результатам прогноза я провожу инверсию масштаба.
Шаг 6. Оценка ошибки прогнозирования
На последнем шаге я вычисляю значения ошибки прогнозирования временных рядов MAE и MAPE.
Величина MAPE оставила около 4%, что показывает в целом адекватность разработанной нейросетевой модели прогнозирования. Однако мы знаем, что это далеко не предел точности! Аналогичное значение MAPE для того же самого временного ряда в отчете за аналогичный период (за 2011 год) составляет около 1.18% при использовании нашей внутренней модели прогнозирования. Подробности можно посмотреть в отчете Точность прогнозирования за истекшие периоды. В упомянутом отчете временной ряд назван для краткости ТГ ЕЦЗ (торговый график европейской ценовой зоны).
Рекуррентная нейронная сеть (RecurrentNeural Network)
1. Рекуррентная структура нейронной сети.
Рекуррентная нейронная сеть используется для прогнозирования данных последовательности (таких как текст, голос, видео, изображения, данные о погоде и акциях и т. Д.). Традиционная нейронная сеть полностью подключена от скрытого слоя к выходному слою, но когда наши данные представляют собой набор Когда есть связанная информация временного ряда, нам необходимо реализовать взаимодействие между внутренними нейронами в скрытом слое, то есть выход скрытого слоя системы останется в сети, и вместе с входом следующего момента системы определить выход следующего момента, и каждый Входной нейрон — это информация момента. Как показано на рисунке ниже, входная информация в каждый момент времени содержит верхний скрытый слой, а также информацию и информацию в этот момент времени.
Проанализируйте внутреннюю часть каждого нейрона скрытого слоя, и каждый нейрон будет обрабатывать исходный ввод и ввод предыдущей временной точки (нейрона) (функция активации tanh), как показано на следующем рисунке:
Прежде чем говорить об обучении RNN, мне нужно поговорить о функции активации tanh, используемой RNN. На самом деле, это очень просто, и это функция гиперболического тангенса. Разница между ней и сигмоидой заключается в том, что она не так чувствительна, как изменение значения функции в интервале (-1, 1). Он менее подвержен градиентной дисперсии при использовании для решения градиента. Обучение RNN аналогично традиционной нейронной сети. При прямом распространении необходимо только вычислить выходное значение каждого момента времени в последовательности во времени. Обратное распространение должно добавить изменения времени в алгоритм BP, которые будут накапливаться с последнего момента Остаток возвращается.
3. Возникла проблема
Как упоминалось выше, для решения явления градиентной дисперсии или градиентного взрыва мы предпочитаем использовать tanh вместо сигмоида, но это может уменьшить вероятность появления только при более низком уровне сети. Как правило, есть две стратегии для решения этой проблемы: 1. В настоящее время функция активации часто используется в нейронных сетях; 2. Улучшить структуру сети, например: LSTM, GRU. В то же время LSTM также способствует решению проблемы долгосрочной зависимости, то есть, когда интервал между соответствующей информацией и текущим прогнозируемым положением становится больше, RNN Восприятие снизится.
Общее описание структуры сети LSTM.
LSTM — это нейронная сеть с рекурсией времени, подходящая для обработки и прогнозирования событий с относительно длинными интервалами и задержками во временных рядах. Системы на основе LSTM могут научиться переводить языки, управлять роботами, анализировать изображения, суммировать документы, распознавать речь, распознавать изображения и писать от руки. Распознавайте чат-ботов и управляйте ими, прогнозируйте болезни, CTR и акции, синтезируйте музыку и многое другое. Причина, по которой LSTM может обрабатывать входную информацию с относительно большой задержкой, заключается в том, что он добавляет ячейку для выбора информации. Каждая ячейка содержит три стробированных структуры и параметр состояния. Состояние ячейки (состояние ячейки), стробированная структура. Чтобы удалить или добавить информацию о состоянии ячейки, он содержит слой сигмоидной нейронной сети и операцию точечного умножения. Далее я объясню три стробирующих структуры и состояния ячеек, а также подробную структуру сети в сочетании со следующим рисунком (это краткое изложение в основном относится к , который является переводом оригинальной статьи, и объяснение очень четкое):
2. Состояние ячейки
Состояние клетки — это Ct, что похоже на состояние клетки и похоже на конвейерную ленту.Информация проходит непосредственно по всей цепочке только с несколькими линейными взаимодействиями.
4. Войдите в ворота.
Входной вентиль определяет, какая информация должна храниться в состоянии ячейки. Входной вентиль состоит из двух частей. Первая часть использует сигмоидальную функцию активации, а выход — это она. Вторая часть использует функцию активации tanh, а выход — это Ct ‘, за которым следует результат обоих Умножит и обновит состояние ячейки.
5. Обновите состояние ячейки.
Старое состояние ячейки умножается на отброшенную информацию ft, и произведение двух типов информации во входном шлюзе добавляется для получения информации Ct в следующий раз.
6. Выходной вентиль
Выходной вентиль определяет, какое значение выводить.Этот вывод будет основан на состоянии нашей ячейки, но это также отфильтрованная версия. Сначала мы запускаем сигмовидный слой, чтобы определить, какая часть состояния ячейки будет выводиться. Затем мы обрабатываем состояние ячейки с помощью tanh (получаем значение от -1 до 1) и умножаем его на результат сигмовидного вентиля. В конце мы выведем только ту часть, которую мы определили для вывода.
Перцептрон
Простейший перцептрон выглядит примерно так:
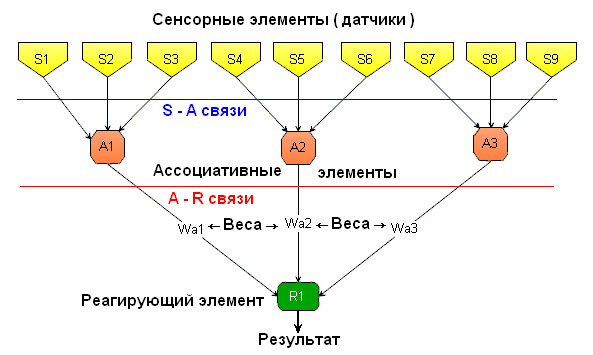
S элементы.
S (или сенсорные) элементы по своей сути представляют собой датчики, считывающие какую то информацию. Эти элементы имеют всего 2 состояния, они либо активны, либо неактивны. Программно можно представить их в виде логической (булевой) функции. Тогда на выходе такой функции будет либо 0 (элемент неактивен) либо 1 (элемент активен)
На рисунке это элементы S1…S9. Таких элементов может быть любое количество. В одном перцептроне может быть несколько групп сенсоров, для различных типов информации
A элементы.
A ( или ассоциативные ) элементы имеют несколько входов, на которые поступают сигналы от сенсоров ( S элементов ) и один выход. Эти элементы также имеют только 2 состояния либо активные, ( если на выходе единица ), либо неактивные ( на выходе ноль ).
А элементы активизируются, если алгебраическая сумма всех входных сигналов превышает какое то пороговое значение.
Например: на рисунке А элементы имеют три входа, на входы элемента А1 подаются сигналы от S элементов S1, S2 и S3. Пусть пороговое значение равно 2. Тогда А элемент активизируется, когда активны 2 из трёх S элементов, независимо от того, какие именно это элементы.
Обычно входов у А элемента гораздо больше, на рисунке изображены только трёх входовые элементы для упрощения. И пороговое значение в какой то степени регулирует чувствительность А элемента.
R элементы.
R ( или реагирующие ) элементы также имеют несколько входов, на которые подаются сигналы от А элементов. Выход R элемента является также выходом перцептрона. Перцептрон может иметь несколько R элементов и соответственно несколько выходов. Выход Rэлемента аналогичен двум предыдущим ( S и R элементам ) то есть имеет тоже 2 состояния ( 0 — неактивен, 1 активен )
R элементы активизируются когда алгебраическая сумма входных сигналов, помноженных на соответствующие им весовые коэффициенты превысит пороговое значение.
A1 * W1 + A2 * W2 + A3 * W3 + … … + An * Wn > pr
где pr это пороговое значение а W1 – Wn веса А связей. Подбирая вес связи мы можем придать какому то сигналу от А элемента большее значение, какому то меньшее, то есть таким образом мы можем обучать нейросеть
Результат работы перцептрона изображённого на первом рисунке несложно просчитать, по сути это обыкновенная логическая микросхема. На следующем рисунке изображён более сложный перцептрон, он также как и первый имеет 9 сенсорных элементов и один выход.
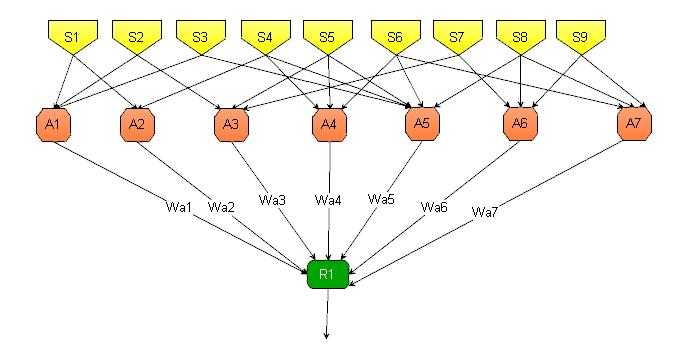
Но в этом перцептроне больше А элементов ( их уже 7 ) Обратите внимание на S связи ( связи между S и A элементами ) Связи расположены совершенно по другому и их гораздо больше. Результат работы такого перцептрона предсказать уже значительно сложнее
По сути он уже способен принимать какие то решения самостоятельно, то есть это уже думающая и обучаемая (хотя и очень примитивно) система.
- Вообще А элементов может быть даже больше чем S элементов. Непосредственно связанные с сенсорами А элементы составляют первый слой перцептрона. Если А элементов достаточно много можно сделать второй, третий и более слой. Таким образом мы можем получить многослойную сеть.
Страницы: 1 Следующая Последняя
